Краткий справочник математических терминов

В этом кратком справочнике поясняются понятия и теоремы, упоминаемые в книгах и задачах, опубликованных на нашем сайте. Справочник ни в кой мере претендует на полноту — это лишь необходимый комментарий к нашим задачам. Справочник формируется в соответствии с запросами наших читателей. Если Вас интересует, что означает данный термин, или что утверждает данная теорема, заполните форму, и мы ответим на Ваш вопрос.

Знаком "*" помечены факты, относящиеся к данному понятию, знаком "-" помечены варианты формулировки определений.

А Б В Г Д З И К Л М Н О П Р С Т У Ф Х Ц Ч Э

Статьи на букву 'М':

Медиана
- треугольника
  Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противоположной стороны треугольника.
  * Медиана треугольника меньше полусуммы, но больше полуразности сторон, между которыми она заключена. (См. задачу 55151.)
  * Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника. (См. задачу 53478.)
  * Средняя линия треугольника, соединяющая середины двух данных сторон, и медиана, проведённая к третьей стороне, делят друг друга пополам.
  * Сумма трёх медиан треугольника меньше периметра, но больше трёх четвертей периметра треугольника. (См. задачу 55161.)
  * Из трёх медиан треугольника всегда можно составить треугольник. (См. задачу 35193.)
  * Если точка лежит внутри треугольника, то сумма квадратов расстояний от неё до вершин треугольника минимальна тогда и только тогда, когда эта точка совпадает с точкой пересечения медиан.
  * Если a, b и c — стороны треугольника, а m_c — медиана, проведённая к стороне, равной c, то
  
  m_c² = $\displaystyle {\textstyle\frac{1}{4}}$ (2a² + 2b² - c²).
  (См. задачу 55267.)
  * Отношение суммы квадратов медиан треугольника к сумме квадратов его сторон равно ${\frac{3}{4}}$ , то есть
  
  $\displaystyle {\frac{m_{a}^{2}+m_{b}^{2}+m_{c}^{2}}{a^{2}+b^{2}+c^{2}}}$ = $\displaystyle {\textstyle\frac{3}{4}}$ .
  (См. задачу 55300.)
  * Медиана треугольника разбивает его на два равновеликих треугольника.
  (См. задачу 54945.)
  * Три медианы треугольника разбивают его на шесть равновеликих треугольников.
  (См. задачу 54957.)
  * Если S — площадь треугольника, а S' — площадь треугольника, стороны которого соответственно равны медианам данного, то
  
  S' = $\displaystyle {\textstyle\frac{3}{4}}$ S.
  
  (См. задачу 54977.)

Многочлен
Многочленом (точнее говоря, многочленом от одной переменной) называют выражение вида
a_nxⁿ+a_n-1x^n-1+...+ a₁x+a₀.

Здесь n — целое неотрицательное число, если a_n ≠ 0, то его называют степенью многочлена. a₀,a₁,...,a_n — числа, их называют коэффициентами многочлена. Если коэффициенты целые, то говорят, что многочлен с целыми коэффициентами, если коэффициенты рациональные — то с рациональными, и т.д.
Многочлены можно складывать, вычитать и перемножать по обычным правилам, приводя подобные слагаемые.
- многочлены Чебышева
  Многочленами Чебышева первого и второго родов соответственно называются многочлены T_n(x) и U_n(x), определяемые равенствами
  
  T_n(cos x)=cos nx, sin x U_n-1(cos x)=sin nx.
  
  Можно показать (задача 61099), что эти равенства действительно определяют многочлены, и что степень T_n и U_n равна n. Некоторые свойства многочленов Чебышева смотри в задаче 61100.
- многочлены Фибоначчи
  Многочлены Фибоначчи F_n(x) (n≥ 0) задаются при помощи начальных условий F₀(x)=0, F₁(x)=1 и рекуррентного соотношения
  F_n+1(x)=x F_n(x)+F_n-1(x) при n≥ 1.
- многочлены Люка
  Многочлены Люка L_n(x) определяются равенствами
  L₀(x)=2, L₁(x)=x L_n+1(x)=x L_n(x)+L_n-1(x) (при n≥ 1).
  
  Некоторые свойства многочленов Фибоначчи и Люка смотри в задачах 61468, 61469, 61470, 61471, 61472.
- многочлены Гаусса
  Многочлены Гаусса g_k,l(x) определяются равенством (для целых неотрицательных k и l):
  
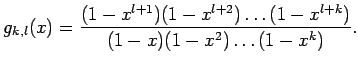
  $\displaystyle g_{k,l}(x)=\frac{(1-x^{l+1})(1-x^{l+2})\ldots(1-x^{l+k})} {(1-x)(1-x^{2})\ldots(1-x^{k})}.$
  
  То, что это многочлены, из определения не видно, это надо доказывать (задача 61522).
  Свойства многочленов Гаусса во многом аналогичны свойствам биномиальных коэффициентов. В частности, среди многочленов они играют ту же роль, что и биномиальные коэффициенты среди чисел. Об этих свойствах, а также о связи многочленов Гаусса с разбиениями натуральных чисел на слагаемые смотри задачи 61521 — 61528.

Момент инерции
Величину I_M = m₁MX₁² +...+ m_nMX_n² называют моментом инерции системы точек X₁,..., X_n с массами m₁,..., m_n относительно точки M.
* Применения этого понятия в геометрии основаны на зависимости I_M = I_O + mOM², где O — центр масс системы, a m = m₁ +...+ m_n.
(Cм. задачи 57765,57772.)

Многоугольник
Простая замкнутая ломаная называется многоугольником, если её соседние звенья не лежат на одной прямой. Вершины ломаной называются вершинами многоугольника. Звенья ломаной назывются сторонами многоугольника. Отрезки, соединяющие несоседние стороны многоугольника, называются диагоналями. Многоугольник с n вершинами, а значит и с n сторонами называется n-угольником.
- вписанный многоугольник
  Выпуклый многоугольник называют вписанным, если все его вершины лежат на одной окружности.
- выпуклый многоугольник
  Есть несколько эквивалентных определений выпуклого многоугольника. Приведем наиболее известные и часто встречающиеся из них. Плоский многоугольник называют выпуклым, если выполнено одно из следующих условий:
  
  — он лежит по одну сторону от любой прямой, соединяющей его соседние вершины (то есть продолжения сторон многоугольника не пересекают других его сторон);
  
  — он является пересечением (то есть общей частью) нескольких полуплоскостей;
  
  — любой отрезок с концами в точках, принадлежащих многоугольнику, целиком ему принадлежит.
  Обычный многоугольник также иногда (не вполне корректно) называют выпуклым, если выпуклым является соответствующий ему плоский многоугольник.
  Углом выпуклого многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине.
  * Сумма углов выпуклого n-угольника равна 180^{o .}(n - 2).
  * Сумма внешних углов выпуклого n-угольника, взятых по одному при каждой вершине, равна 360^o.
- описанный
  Выпуклый многоугольник называют описанным, если все его стороны касаются некоторой окружности.
- плоский
  Говоря неформальным языком, основное отличие плоского многоугольника от обычного состоит в том, что обычный многоугольник — это лишь контур, а плоский многоугольник состоит из точек, лежащих внутри контура (и на самом контуре). Дадим теперь формальное определение. Рассмотрим многоугольник M. M разбивает всю плоскость на две области M_I и M_E, так что
  1) Множества M, M_I и M_E не пересекаются;
  2) Объединение множеств M, M_I и M_E составляет всю плоскость.
  3) Любые две точки как множества M_I, так и множества M_E, можно соединить ломаной, целиком содержащейся в M_I и M_E соответственно.
  4) Любая ломаная, у которой один из концов лежит в M_I, а другой — в M_E, пересекает M.
  5) Ровно одно из множеств M_I и M_E ограничено (то есть содержится в некотором круге).
  Эти утверждения несложно вывести, например, из Леммы Жордана. Пусть M_I — то из множеств M_I и M_E, которое ограничено. Плоским многоугольником, ограниченным многоугольником M, называют объединение множеств M и M_I. В данном случае также говорят, что M является границей (контуром) соответствующего плоского многоугольника.
  Отметим, что гораздо более полезным (и уболее удобным в использовании) математическим понятием является понятие "простой фигуры" на плоскости.
- правильный
  Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.
  * Правильный выпуклый многоугольник является вписанным в окружность и описанным около окружности.
  * При одинаковом количестве сторон правильные многоугольники подобны. В частности, если у них стороны одинаковы, то многоугольники равны.

От кого (e-mail):
Что Вас интересует: