А Б В Г Д З И К Л М Н О П Р С Т У Ф Х Ц Ч Э
Статьи на букву 'О':
Выпуклой оболочкой данной фигуры
называется наименьшее выпуклое множество, содержащее данную фигуру.
"Наименьшее множество" здесь означает наименьший элемент по отношению к вложению множеств, то есть такое выпуклое множество, содержащее данную фигуру, что оно содержится в любом другом выпуклом множестве, содержащем данную фигуру.
* У любой фигуры есть ровно одна выпуклая оболочка — это пересечение всех выпуклых фигур, содержащих данную фигуру.
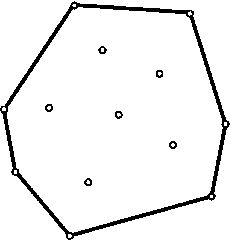
* Выпуклой оболочкой конечного набора точек на плоскости (в том числе и вершин невыпуклого многоугольника) всегдя является выпуклый плоский многоугольник (в вырожденных случаях — отрезок или точка), причем его вершины являются подмножеством исходного набора точек (см. рис.). Аналогичный факт верен и для конечного набора точек во многомерном пространстве.
Окружностью называется геометрическое место точек плоскости, удалённых
от данной точки плоскости, называемой центром окружности, на данное положительное расстояние,
называемое радиусом окружности. Радиусом называется также любой отрезок, соединяющий
точку окружности с центром. Хордой окружности называется отрезок, соединяющий две точки окружности.
Хорда, проходящая через центр, называется диаметром окружности.
См. также "круг".
* Диаметр, перпендикулярный хорде, делит её пополам. (См. задачу 53911)
* Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде. (См. задачу 53912)
* Серединный перпендикуляр к хорде проходит через центр окружности.
* Замечательное свойство окружности: Геометрическое место точек, из которых отрезок AB виден под прямым углом, есть окружность с диаметром AB без точек A и B. (См. задачу 53925.)
* Уравнение окружности: Уравнение окружности радиуса R с центром в точке M(x0;y0) в декартовых координатах xOy имеет вид
* Длина окружности: Окружность радиуса R имеет длину 2πR.
Рассмотрим две различные точки A и B на плоскости. Геометрическое место точек M,
для которых AM : BM = k (k > 0) является окружностью, которая называется окружностью Аполлония.
(См. задачи 54550,57142.)
Треугольник с вершинами в постоянных точках треугольника
называют треугольником Брокара, а описанную окружность
этого треугольника (то есть окружность подобия треугольника) —окружностью Брокара.
Диаметр KO этой окружности называют диаметром Брокара.
Вневписанной окружностью треугольника называется окружность, которая касается
стороны треугольника и продолжений двух других его сторон (то есть она касается прямых, содержащих
стороны треугольника, причём одна из точек касания лежит на стороне треугольника, а две другие —
на продолжениях его сторон).
* Биссектрисы двух внешних и третьего внутреннего угла треугольника пересекаются в одной точке, которая является центром вневписанной окружности треугольника.
* Для любого треугольника существует единственная вневписанная окружность, касающаяся данной его стороны.
* Если вневписанная окружность треугольника ABC, касается продолжения стороны AB в точке M, то AM = p, где p — полупериметр треугольника ABC. (См. задачу 55483.)
* Если вписанная и вневписанная окружности треугольника ABC, касаются стороны BC в точках M и N, то BM = CN.
Окружность называется вписанной в угол, если она касается
сторон этого угла (то есть она касается прямых, содержащих стороны угла, причём точки
касания лежат на сторонах угла).
* Центр окружности, вписанной в угол, лежит на биссектрисе этого угла. (См. задачу 53960.)
Окружность, называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.
* Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности. Сам многоугольник в таком случае называется описанным около данной окружности. Таким образом, в выпуклый многоугольник можно вписать не более одной окружности.
* В каждый треугольник можно вписать окружность, притом ровно одну. Ее центр — это точка пересечения биссектрис треугольника.
* Если окружность, вписанная в треугольник ABC, касается стороны AB в точке M, то AM = p - BC, где p — полупериметр треугольника ABC. (См. задачу 52554.)
* Если вписанная и вневписанная окружности треугольника ABC, касаются стороны BC в точках M и N, то BM = CN.
* В выпуклый четырехугольник ABCD можно вписать окружность тогда и только тогда,
когда суммы его противоположных сторон равны:
AB + CD = AC + BD.
(См. задачи 52645,52699.)
В каждом треугольнике следующие девять точек:
середины сторон, основания высот и середины отрезков, соединяющих точку пересечения высот
с вершинами, лежат на одной окружности. Эта окружность называется
окружностью девяти точек данного треугольника.
*
Если H — точка пересечения высот данного треугольника, а O — центр его описанной окружности, то
центром окружности девяти точек является середина отрезка OH.
(См. задачу 56958.)
См. "инверсия на плоскости".
Приведем два эквивалентных определения касания окружностей:
— Говорят, что две различные окружности, имеющие общую точку, касаются
в этой точке, если они имеют в этой точке общую касательную.
— Говорят, что две окружности касаются, если они имеют единственную общую точку.
* Линия центров двух касающихся окружностей проходит через их точку касания. (См. задачу 53994.)
Через точку Лемуана данного треугольника проведем прямые,
параллельные сторонам этого треугольника. Окружность, проходящая через
точки их пересечения со сторонами треугольника (в общем случае таких точек 6), называется
первой окружностью Лемуана.
Если же через точку Лемуана провести прямые, антипараллельные сторонам
треугольника, то окружность, проходящая через точки их пересечения со сторонами треугольника называется
второй окружностью Лемуана.
(См. задачу 56990.)
Пусть вершины B и C треугольника фиксированы, а
вершина A движется так, что угол Брокара ![]() треугольника ABC
остается постоянным. Тогда точка A движется по окружности радиуса
(a/2)
треугольника ABC
остается постоянным. Тогда точка A движется по окружности радиуса
(a/2)![]() , где a = BC, которая и называется
окружностью Нейберга.
, где a = BC, которая и называется
окружностью Нейберга.
(См. задачу 56976.)
Окружность, называется описанной вокруг (около) выпуклого многоугольника,
если все вершины данного многоугольника расположены на этой окружности.
Сам многоугольник в таком случае называется вписанным в данную окружность.
* Если вокруг данного выпуклого многоугольника можно описать окружность, то серединные перпендикуляры к его сторонам пересекаются в одной точке, которая является центром описанной окружности. Таким образом, вокруг выпуклого многоугольника можно описать не более одной окружности.
* Вокруг каждого треугольника можно описать окружность, притом ровно одну. Ее центр — это точка пересечения серединных перпендикуляров в сторонам треугольника.
* Вокруг выпуклого четырехугольник ABCD можно описать окружность тогда и только тогда,
когда суммы его противоположных углов равны 180o:
![]() ABC +
ABC + ![]() CDA = 180o =
CDA = 180o = ![]() BCD +
BCD + ![]() DAB.
DAB.
(См. задачи 52344,52387.)
Пусть A1, B1 и C1 — основания перпендикуляров, опущенных из
точки P на прямые BC, CA и AB. Треугольник A1B1C1 называют
подерным (или педальным) треугольником
точки P
относительно треугольника ABC. Описанную окружность подерного треугольника
называют подерной (или педальной)
окружностью.
См. "треугольник подобия".
треугольника ABC, если она проходит через точки пересечения сторон треугольника ABC с продолжениями
сторон треугольника A'B'C', полученного из треугольника ABC при гомотетии с центром в точке Лемуана K.
Эти точки (в общем случае их шесть) всегда лежат на одной окружности.
(См. задачу 56988.)
*
Центр окружности Тукера лежит на прямой KO, где K - точка Лемуана, O - центр описанной окружности.
(См. задачу 56989.)
Опустим из точки M перпендикуляры MA1, MB1 и
MC1 на прямые BC, CA и AB. Для фиксированного треугольника ABC
множество точек M, для которых угол Брокара треугольника A1B1C1 имеет
заданное значение, состоит из двух окружностей, причем одна из них расположена
внутри описанной окружности треугольника ABC, а другая вне ее. Данные окружности называются
окружностями Схоуте треугольника ABC.
(См. задачу 56977.)
Ортотреугольником данного непрямоугольного треугольника называется
треугольник, вершины которого — основания высот данного треугольника.
* Свойство ортотреугольника: Высоты остроугольного треугольника являются биссектрисами углов его ортотреугольника. Высоты тупоугольного треугольника являются биссектрисами двух внешних и одного внутреннего углов его ортотреугольника. (См. задачу 52866.)
* Признак ортотреугольника: Пусть на сторонах AB, BC и CA остроугольного треугольника ABC взяты точки C1, A1 и B1 соответственно. При этом
Ортоцентром треугольника называется точка пересечения прямых,
содержащих высоты данного треугольника.
* В любом треугольнике такая точка существует и единственна. (См. задачу 53527.)
* Расстояние от ортоцентра до вершины треугольника вдвое больше расстояния от центра описанной окружности треугольника до стороны, противолежащей данной вершине. (См. задачу 53528.)
* Точка, симметричная ортоцентру относительно прямой, содержащей сторону треугольника, лежит на описанной окружности треугольника. (См. задачу 55463.)
Ось Ox прямоугольной системы координат, в которой уравнение параболы имеет вид y2 = 2px,
называют осью параболы. Ясно, что ось параболы является её осью симметрии.
См. "треугольник подобия".
Рассмотрим две неконцентрические окружности на плоскости: S1 и S2. Геометрическим местом точек,
для которых степень относительно S1 равна степени относительно S2, является прямая, которая
называется радикальной осью окружностей S1 и S2.
см. задачу 56714
См. "осевая симметрия".
Отрезком называется часть прямой, которая состоит из всех точек
этой прямой, лежащих между двумя данными её точками. Эти точки называются
концами отрезка.
* Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
* На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один.
Два отрезка называются равными, если они имеют одинаковую длину.
См. "двойное отношение".
Пусть
![]() и
и
![]() — коллинеарные векторы.
Ориентированным отношением
— коллинеарные векторы.
Ориентированным отношением
![]() отрезков
(правильнее было бы говорить об ориентированном отношении ориентированных коллинеарных отрезков)
отрезков
(правильнее было бы говорить об ориентированном отношении ориентированных коллинеарных отрезков)
![]() и
и
![]() называется
величина
±
называется
величина
±![]() , где знак плюс берется в том случае, когда векторы
, где знак плюс берется в том случае, когда векторы
![]() и
и
![]() сонаправлены, а знак минус — в случае, когда векторы
сонаправлены, а знак минус — в случае, когда векторы
![]() и
и
![]() направлены в разные стороны.
направлены в разные стороны.
